CF2050F Maximum modulo equality 题解
0x00 题目翻译
有一个长度为 的序列 和 个询问,每个询问给出一个区间 要求查询最大的 使得这个区间里所有数字模 的结果相同(如果 可以取得无穷大,输出 )。
0x01 解题思路
这里要求余数全部相同,这样入手不好分析,那么尝试反向思考:如果余数已经相同, 已经确定,那么序列会有什么性质?
设原序列为 ,那么可以表示为 ,其中 是那个相同的余数。
观察到每一项带有相同的 ,尝试将它消掉,可以将相邻两项做差,求出一个差分序列 ,即 $0,\vert a_1-a_2\vert ,\vert a_2-a_3\vert ,\cdots,\vert a_{n-1}-a_n\vert $,也就是 $0,\vert k_1-k_2\vert m,\vert k_2-k_3\vert m,\cdots,\vert k_{n-1}-k_n\vert $,这时,就可以用 的区间最大公约数求出最大的 (序列 开头的 只是在写代码时和 对齐位置,没有意义)。
0x02 算法实现
似乎大部分人用的是 ST 表,但这里我用的是线段树(因为不会 ST 表),只有查询,没有修改,是比较好写的。
0x03 易错要点
- 输入的查询区间不是 中的区间,应为 。
- 注意当 时要特判,否则你的实际查询会 导致 RE。
- 建树时可以只用 的一段数值传入,但同样应注意 的情况。
0x04 程序代码
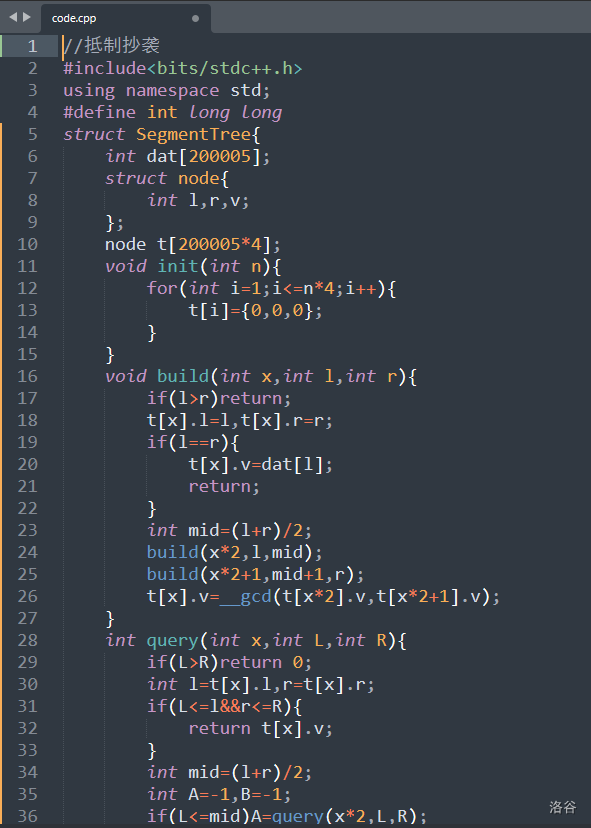
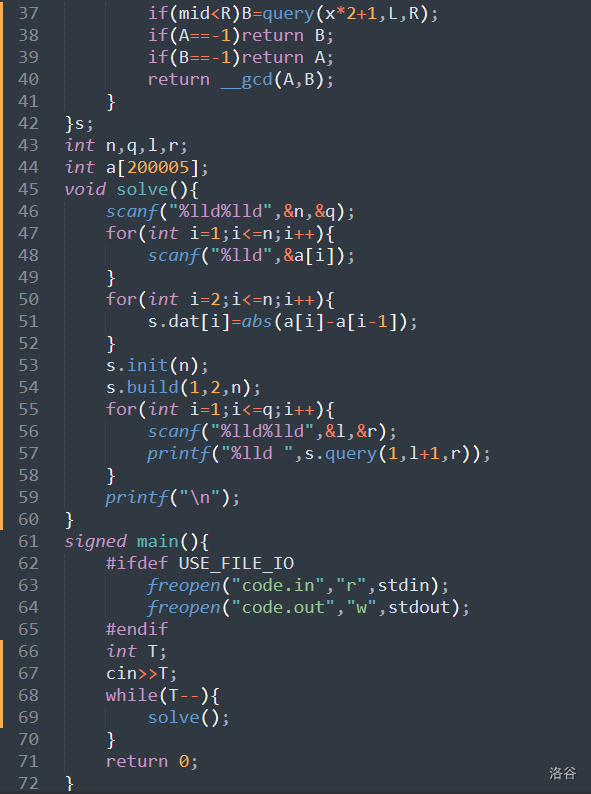
CF2050F Maximum modulo equality 题解
https://shicj.pages.dev/2024/12/27/CF2050F Maximum modulo equality 题解/