第八课 复数
1. 复数的定义
-
复数集
\C=\{a+bi\vert a,b\in\R\}
-
代数形式
z=a+bi
- a 称为实部 Re(z)=a
- b 称为虚部 Im(z)=b
- i 称为虚数单位 i2=−1
- b=0 为实数
- b=0 为虚数(a=0 为纯虚数)
-
几何形式:复平面
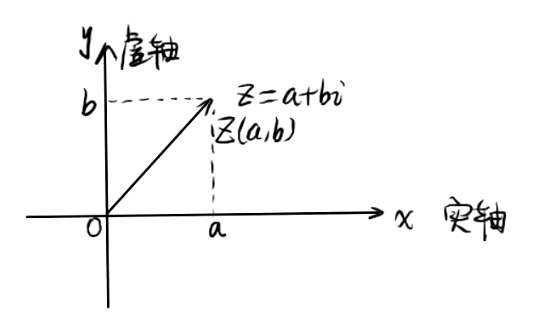
复数与复平面上的点、平面向量一一对应
-
模
z=a+bi
∣z∣=a2+b2
-
共轭复数
实部相同,虚部互为相反数的复数互为共轭复数
z=a+bi
z=a−bi
-
共轭复数的性质
∣z∣=∣z∣
z+z=2a
z−z=2bi
z⋅z=a2+b2=∣z∣2∈R
z1+z2=z1+z2
z1−z2=z1−z2
(z2z1)=z2z1
2. 复数的代数运算
设 z1=a+bi,z2=c+di
-
加法
z1+z2=a+c+(b+d)i
-
减法
z1−z2=a−c+(b−d)i
-
数乘
λz1=λa+λbi
-
乘法
z1z2=ac−bd+(ad+bc)i
-
除法
z2z1=(c+di)(c−di)(a+bi)(c−di)
3. 复数的三角表示
-
定义
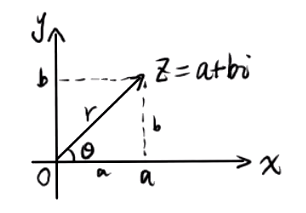
a=rcosθ,b=rsinθ,z=a+bi=r(cosθ+isinθ)
θ 是幅角(不唯一),θ∈[0,2π) 的幅角,称为幅角的主值,记 argz∈[0,2π)
r 是模长,r=a2+b2
-
乘法
z1z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]
模长相乘,幅角相加
-
除法
z2z1=r2r1[cos(θ1−θ2)+isin(θ1−θ2)]
模长相除,幅角相减
-
模的性质
∣z1⋅z2∣=∣z1∣∣z2∣
∣z2z1∣=∣z2∣∣z1∣
推广:∣z∣n=∣zn∣

