高中数学笔记-7-平面向量
第七课 平面向量
1. 向量基础知识
-
定义
-
向量:既有大小,又有方向的量
-
数量:只有大小,没有方向的量
-
零向量:长度为 的向量,表示为 ,方向任意
-
单位向量:长度等于 个单位的向量,即
-
相等向量:长度相等且方向相同的向量
-
相反向量:长度相等且方向相反的向量,即
-
平行向量:方向相同或相反的非零向量,零向量与任何向量平行,没有传递性
-
-
向量的表示
-
几何表示(有向线段)
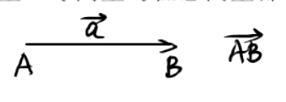
-
小写字母()
-
坐标()
-
2. 向量的运算
-
向量加法运算
-
三角形法则:首尾相连,由首至尾
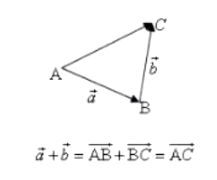
-
平行四边形法则:共起点
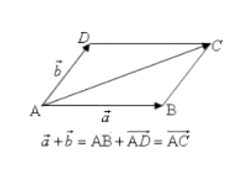
-
向量三角不等式:
-
-
向量减法运算
-
三角形法则:共起点,连终点,方向指向被减向量
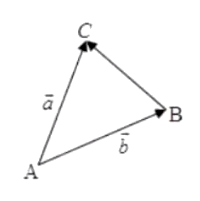
-
-
向量数乘运算
- 实数 与向量 的积是一个向量,记作
- 当 时, 的方向与 的方向相同,当 时, 的方向与 的方向相反,当 时,
-
向量的数量积和投影
-
,零向量与任意向量的数量积为
-
与 同向
-
与 反向
-
为锐角 且 与 不共线
-
为钝角 且 与 不共线
-
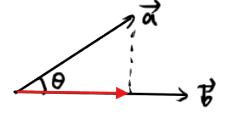
投影: 在 方向上的投影为 或 ,投影是一个数值,可正可负可零
-
数量积的几何意义: 的长度与 在 方向上的投影的乘积
-
投影向量: 在 方向上的投影向量为 或
-
性质:
-
运算律1:
-
运算律2:
-
运算律3:
-
注意:没有分配律!
-
3. 平面向量和坐标
-
向量的坐标
选定 为基底(通常是垂直的),令 ,
若 ,则把有序数对 叫做 的坐标
-
向量的坐标运算
令 ,
-
分点坐标公式
设点 是线段 上的一点,,,当 时,点 的坐标为
4. 平面向量有关定理
-
向量共线定理
-
向量 ,当且仅当存在唯一一个实数 ,使得
-
推论1:、、 三点共线 、 共线
-
推论2:向量 、、 三终点 、、 共线 存在实数 、,使得 ,且
-
-
基底
-
如果 、 是同一平面内的两个不共线的向量,呢么对于这个平面内的任意向量 ,有且只有一对实数 、,使得 ,其中 、 是一组基底
-
注意:零向量不能作为基底
-
-
极化恒等式
- 几何意义:以 和 为邻边的平行四边形的两条对角线长度的平方差乘以
- 使用特点:两向量的和或差的模已知时
-
对角线向量公式(斯坦纳公式)
-
三角形结论
5. 平面向量与三角形四心
-
为 重心
-
设 ,,,则 的重心坐标为
-
面积比与四心结论1(奔驰定理)
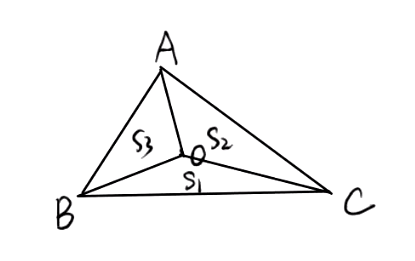
设 是 内任意一点,,, 的面积分别为 ,, 则
-
面积比与四心结论2
设 是 内任意一点,,, 的面积分别为 ,,
- 当点 与点 在 异侧时,则
- 当点 与点 在 异侧时,则
- 当点 与点 在 异侧时,则
6. 平面向量的应用
-
正弦定理
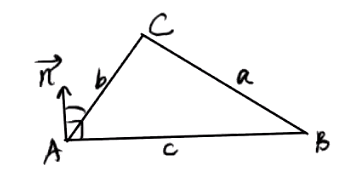
如图,取与 垂直且向上的一个单位向量
同理可证:
-
余弦定理
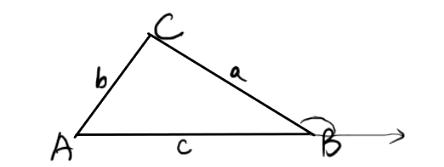
同理可证出另外两组边角
余弦定理的向量式: