高中数学笔记-1-函数的概念及其表示
第一课 函数的概念及其表示
1. 函数的概念
一般的,设 是非空的实数集(),如果对于集合 中的任意一个数 ,按照某种确定的对应关系 ,在集合 中都有唯一确定的数 和它对应,那么就称 为从集合 到集合 的一个函数,记作
其中,叫做自变量, 的取值范围 叫做函数的定义域;与 值相对应的 值叫做函数值,函数值的集合 叫做函数的值域。
函数的三要素(两域一关系):定义域、值域、对应关系(对应法则)
映射(教材已删去):与函数类似,但映射研究任意非空集合,函数是特殊是映射。
例题:存在函数 满足,对任意 都有()?
A. ,B. C. D.
根据函数的概念解题
A. 当 和 时,函数值相同,不符合。
B. C. 同理,略去
D. 令 ,解出 ,即 ,满足。
注意:换元法,新元范围要写上
2. 求函数的定义域
-
定义域、值域的书写:区间
闭区间
开区间
左闭右开区间
左开右闭区间
注意:无穷大取不到,要写开区间。
-
判断函数相同
值域由定义域、对应关系决定,所以只要定义域、对应关系相同即为同一个函数。
-
具体函数定义域
平方根里为负数,分母为 ,。
以上情况要在定义域里排除,根据条件列不等式求解。
分式:
-
抽象函数(复合函数)定义域
列不等式限制,注意定义域始终是 (或其他字母)的范围。
例题:若函数 的定义域为 ,求函数 的定义域。
注意:定义域 是 的范围。
中 ,所以 的定义域为 ,代入 求定义域即可。
答案:
-
求参数范围
转换为恒成立问题,利用判别式、图像求解。
例题:已知函数 的定义域为 ,求 的范围。
转化: 在 上恒成立。
当 时,,满足。
当 时,(根据图像判断),解得 。
综上所述,
3. 求函数的值域
-
配方法
例题:
-
换元法
例题:
令
配方法
-
分离常数法(一次比一次)
例题:
-
分离常数法+范围限定
例题:
也可用 表示 求解(反表示法)
-
图像法之一次比一次
例题:
双曲线画图象,先找渐近线:(极限思想很方便)
再代入一个点(确定位置),比如 。
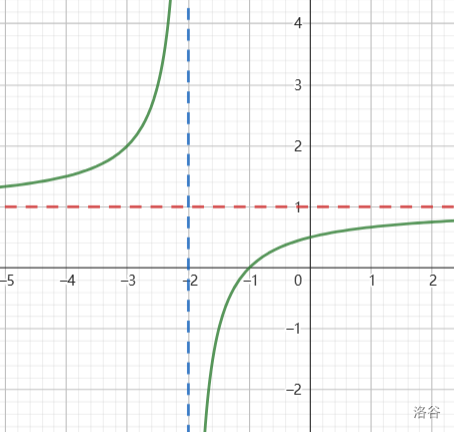
然后在图像上截取,得到
-
方程思想(主元法,二次比二次)
例题:
方程思想
以 为主元
-
当 即 时,
-
当 时,要使得关于 的一元二次方程有解
解得
此时 且
综上所述
-
-
图像法之对勾函数、飘带函数(基本不等式也可)
对勾函数:
渐近线
极值点:
渐近线
极值点:
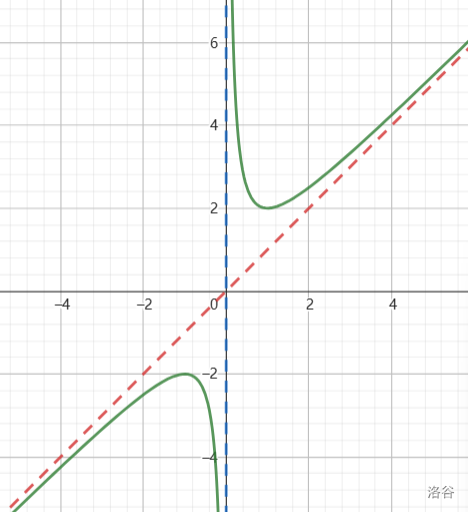
飘带函数:
渐近线
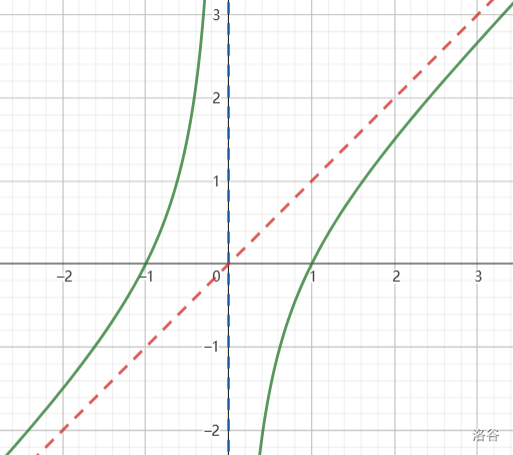
例题:
分离常数法
换元法
令
利用对勾
一步步限制得到答案:
-
图像法之含参问题
画出图像,分段进行分类讨论。
4. 求函数解析式
-
换元法(注上新元范围)(推荐)
例题:已知 ,求函数 的解析式。
令 ,即
-
配凑法
-
赋值法
例题:已知 ,求函数 的解析式。
令 为
-
已知类型的复合函数
例题:已知一次函数 满足 ,求 的解析式。
令
解得 或
即 或
-
消元法(解方程)
注:有时列一个方程不够,可以列多个。
例题:已知 ,求 的解析式。
令 为 ,得
与已知条件联立,得到