CF2001C Guess The Tree 题解
0x00 题目翻译
一棵有 个节点的秘密树,索引从 到 ,并要求你使用以下类型的查询来猜测它:
- “? a b” - Misuki 会告诉你哪个节点 使 最小,其中 是节点 和 之间的距离。如果存在多个这样的节点,那么 Misuki 会告诉你哪个节点能使 最小化。
用最多 次查询找出秘密树的结构!
0x01 解题思路
由距离差最小值,想到中点,由 次查询,想到 ,于是自然想到类似二分的思想。
什么时候可以确定一条边呢?当我们查询到两个相邻节点(中间有边)时,答案必定是这两个节点中的一个。反推,如果查询到答案是传入的两个点中的一个,这两个点中间有一条边。
这是只需要以 次查询,确定 条边,即完成此题。
首先钦定一个根节点,因为是树,所以任何一个点都可以作为根节点,于是直接令 节点为根,如图为例。
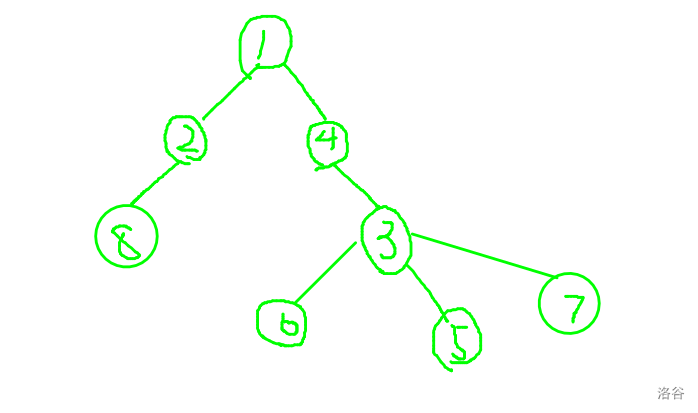
容易想到可以尝试遍历除根节点之外的所有点,对于每个点, 次操作确定它和它父亲之间的边。
每次查询得到起点到当前点路上的中点,开始时以根为起点,之后每次以上一次查询的结果为起点,最终当答案为这一次查询的起点时,即可确定当前点与这个点之间有边。(上文中语义可能有点不清,当前点指的是当前遍历到的点)。
具体的例子:
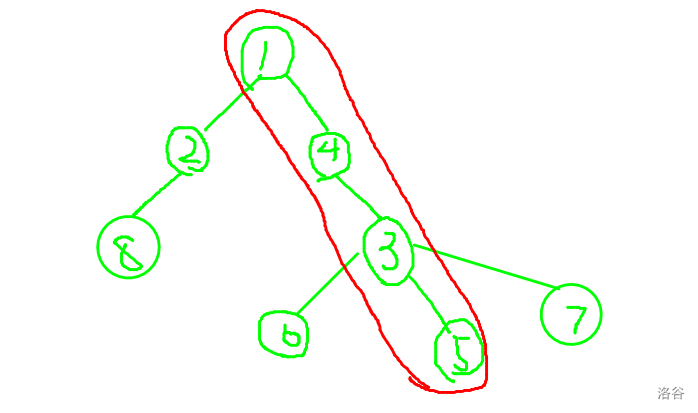
令根为 ,当前点为 。
- 第一次查询 ,得到这条路上的中点为 ,因为 ,所以继续。
- 第二次查询 ,得到这条路上的中点为 ,因为 ,所以继续。
- 第三次查询 ,得到这条路上的中点为 ,因为 ,所以确定有边 。
这实际上就是二分查询,易证复杂度。
0x02 AC Code
1 | |
CF2001C Guess The Tree 题解
https://shicj.pages.dev/2024/08/25/CF2001C Guess The Tree 题解/